Acquisition comprimée

Rappel

Qu’est ce qu’une norme

La norme l0

Optimisation l0

Le but de la régularisation est d’imposer une solution unique à un problème mal formulé qui a une infinité de solutions.

La norme l1

La norme l1 de x est défini tel que :

${ \| {\vec {x}}_{1} \| = \|x_{1}\| + \ldots + \|x_{n} \|}$

Elle est donnée par la somme des modules (ou valeurs absolues) des coefficients et induit la distance de déplacement à angle droit sur un damier, dite distance de Manhattan

La norme l2

La norme l2 est la plus populaire :

$\|{\vec {x}}\|_{2}={\sqrt {|x_{1}|^{2}+\ldots +|x_{n}|^{2}}}$

Nommée aussi norme euclidienne, elle est obtenue à partir du produit scalaire et correspond à la norme habituellement utilisée pour la distance entre deux points dans le plan ou l’espace usuels.

Optimisation l2

La régularisation la plus simple à étudier est du type norme L2, qui se réduit à un problème linéaire. Un modèle linéaire amène des optimisations quadratiques

Le problème de minimiser la norme l2 peut-être formulé comme:

$min {\left \| x \right \|}_2$ tel que $Ax = b$

Assume that the constraint matrix A has full rank, this problem is now a underdertermined system which has infinite solutions. The goal in this case is to draw out the best solution, i.e. has lowest l_2-norm, from these infinitely many solutions. This could be a very tedious work if it was to be computed directly. Luckily it is a mathematical trick that can help us a lot in this work.

By using a trick of Lagrange multipliers, we can then define a Lagrangian

${\mathfrak{L}(\boldsymbol{x})} = {\left \| \boldsymbol{x}\right\|}_2^2+\lambda^{T}(\boldsymbol{Ax}-\boldsymbol{b})$

where $\lambda$ is the introduced Lagrange multipliers. Take derivative of this equation equal to zero to find a optimal solution and get

$\hat{\boldsymbol{x}}_{opt} = -\frac{1}{2} \boldsymbol{A}^{T} \lambda$

plug this solution into the constraint to get

$\boldsymbol{A}\hat{\boldsymbol{x}}_{opt} = -\frac{1}{2}\boldsymbol{AA}^{T}\lambda=\boldsymbol{b}$ $\lambda=-2(\boldsymbol{AA}^{T})^{-1}\boldsymbol{b}$

and finally

${\hat{\boldsymbol{x}}}_{opt}=\boldsymbol{A}^{T} (\boldsymbol{AA}^{T})^{-1} \boldsymbol{b}={\boldsymbol{A}^{+} \boldsymbol{b}}$

By using this equation, we can now instantly compute an optimal solution of the l_2-optimisation problem. This equation is well known as the Moore-Penrose Pseudoinverse and the problem itself is usually known as Least Square problem, Least Square regression, or Least Square optimisation.

However, even though the solution of Least Square method is easy to compute, it’s not necessary be the best solution. Because of the smooth nature of l_2-norm itself, it is hard to find a single, best solution for the problem.

L’approche classique pour résoudre un système d’équations linéaires surdéterminées exprimées par

$A\mathbf {x} =\mathbf {b}$

est connue comme la méthode des moindres carrés et consiste à minimiser le résidu

$\|A\mathbf {x} -\mathbf {b} \|^{2}$

où $\|\cdot \|$ est la norme euclidienne.

L1, en général, tu dois utiliser des approximations et des descente de gradient

quand on régularise on change la fonction à minimiser, c’est un peu comme si on donnait un a priori sur quels x nous plaisent plus que d’autres : pour être rigoureux sur cette histoire d’a priori en général on part sur une formulation probabiliste/statistique
la régularisation L2 veut une norme L2 de x pas trop grande, ça s’interprète bien comme une histoire d’énergie ou même de filtrage. en supposant les données suivant une loi gaussienne (données bruitées) on tombe sur le problème d’optimisation quadratique régularisé L2.
un problème quadratique régularisé L2 reste un problème quadratique : on a donc un moyen facile de trouver la solution (minimum local de g(x) puis simplexe si pas de minimum local)
la régularisation L1 ou L0 (ou même L3/2) est un autre type de régularisation. l’apriori qu’on a sur x est qu’il est sparse (contient beaucoup de valeurs nulles ou presque nulles) la régularisation L1 est pratique quand on a la contrainte x_i >= 0, dans ce cas ça reste un problème quadratique
sinon la régularisation L1 introduit des problèmes de calculs : minimum locaux / fonction non convexe / non dérivable.
le “kernel trick” s’applique aux problèmes quadratiques, mais pas trop aux autres (il faut que x soit dans le sous espace engendré par les données pour appliquer le kernel trick)

http://forums.futura-sciences.com/mathematiques-superieur/644866-comparaison-de-methodes-de-regularisations.html

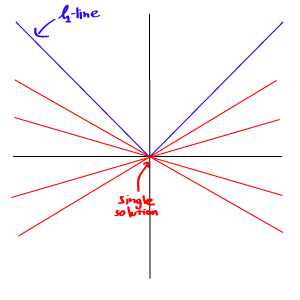
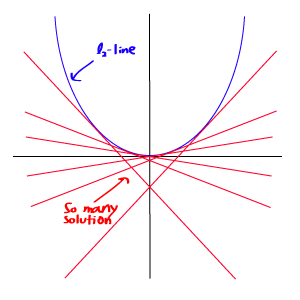
https://fr.wikipedia.org/wiki/R%C3%A9gularisation_Tychonoff

https://rorasa.wordpress.com/2012/05/13/l0-norm-l1-norm-l2-norm-l-infinity-norm/

Traduction approximative de l’article de Lustig, MRM

Nous allons maintenant décrire plus en détail le processus de reconstruction non linéaire d’image adapté à l’acquisition comprimée.Considérons l’image en question est un vecteur noté $m$ , ${\Psi}$ l’opérateur linéaire qui transforme un pixel en sa représentation “sparse” et tel que $\mathscr{F}_{u}$ est la transformée de Fourier sous échantillonné, correspondant à un motif de l’espace réciproque sous échantillonnée présenté précedemment. La reconstruction est obtenu en résolvant le problème suivant d’optimisation sous contrainte.

Minimisons ${\left\|{\Psi}m\right\|}_{1}$ tel que ${\left\|\mathscr{F}_{u}m-y\right\|}_{2} < \epsilon$

Ici $m$ est l’image reconstruite, $y$ est la mesure dans l’espace réciproque effectué par le scanner et $\epsilon$ est le terme d’attache au donnée qui contrôle la fidélité de la reconstruction vis à vis des données mesurées. Le seuil $\epsilon$ est généralement fixé en dessous du niveau de bruit attendu.

La fonction “objective” dans l’équation précédente est une norme $l_{1}$ qui est définie comme ${\left\|x\right\|}_{1}= {\sum_{i} {| x_{i} |}}$ . Minimiser ${\left\|{\Psi}m\right\|}_{1}$ favorise la “sparisité”. La contrainte ${\left\|\mathscr{F}_{u}m-y\right\|}_{2} < \epsilon$ contraint l’attache au données. En d’autres mots, parmis toutes les solutions qui sont consistantes avec les données acquises, l’équation [3] trouve la solution qui est la plus compressible par la transformation ${\Psi}$ .

De nombreux problèmes de régularisation basé sur une norme L1 reste difficile à résoudre

Cet article se situe dans le dossier _posts. Allez l’éditer, et générez votre site à nouveau pour voir les modifications. Vous pouvez générer le site de différentes façons, mais le plus efficace est de lancer la commande jekyll serve, qui crée un serveur web et génère automatiquement votre site à chaque fois qu’un fichier est modifié.

Pour ajouter un autre article, créez un nouveau fichier dans le dossier _posts dont le nom contient la date de la façon suivante : AAAA-MM-JJ-nom-de-l-article.ext et placez-y l’entête. includes the necessary front matter. Regardez le code source de cet article pour avoir une bonne idée de la façon dont cela fonctionne.

Jekyll permet aussi d’intégrer des extraits de code :

def print_hi(name)
  puts "Bonjour, #{name}"
end
print_hi('Tom')
#=> affiche 'Bonjour, Tom' sur STDOUT.

Jetez un coup d’oeil à la documentation de Jekyll pour en savoir plus sur ce qu’il vous est possible de faire avec Jekyll. Tous les bugs et demandes de fonctionnalités doivent être envoyés sous forme de requête sur GitHub. Si vous avez des questions, allez les poser sur le fil d’aide de Jekyll.

$\sqrt{27}$ $\frac{\partial f} {\partial x} $ \quad $ $ \frac{\partial f}{\partial x} $$ $H_{2} O is a liquid. 2^10^ is 1024.$ $\mathscr{F}$

TV/ROF Denoising:

$min {\left\|u\right\|}_{BV} + \frac{\mu}{2} \left\|u-f\right\|^{2}_{2}$